Word Embeddings
Word embeddings is to learn a vector representation of a word.
Table of contents
Necessity
One-hot vector representation
Previously, we used one-hot vector to represent different words. One-hot vector means a vector with only one “1” and others are all zeros. However, this method soon encounters some problems…
- When a word set gets larger, the dimension of the vector grows too big.
- We cannot express similarities between two words because inner product of two one-hot vectors are “0”.
- Therefore, poor efficiency in computation and learning.
Word embedding
To cope with one-hot vector approach, word embedding is used. In a nutshell, word embedding is featurized representation of words.
- One can adjust dimension(= numbers of features) of word vectors.
- In contrast to binary one-hot vector, word embedding approach maps words into low dimensional real numbers.
- Improves computational and learning efficiency.
- Most importantly, this approach can capture similarities between words!
Idea
The idea of word embedding is to learn a embedding matrix like below: 1
| Man(5931) | Woman(9853) | King(4914) | Queen(7157) | Apple(456) | Orange(6257) | |
|---|---|---|---|---|---|---|
| Gender | -1 | 1 | -0.95 | 0.97 | 0.00 | 0.01 |
| Royal | 0.01 | 0.02 | 0.93 | 0.95 | -0.01 | 0.00 |
| Age | 0.03 | 0.02 | 0.70 | 0.69 | 0.03 | -0.02 |
| Food | 0.09 | 0.01 | 0.02 | 0.01 | 0.95 | 0.97 |
Note that subtraction of two opoosite words e_man - e_woman is almost similar to e_king - e_queen as [-2 0 0 0] ~ [-2 0 0 0].
Analogies using word vectors
Word embedding similarity figure2
Let’s say we plot two pairs of words in the number of feature, n-dimensioned space. Then, we can aswer to the question:
e_man - e_woman ~ e_king - e_w
by simply doing vectore calcuation such that:
find word w: arg max_w sim(e_w, e_king - e_man + e_woman)
This is possible because of the Parallelogram Relationship between two vectors. To compute similarity of two vectors, we can think of four methods.
- Cosine Similarity
- Eucilidean Distance (L2 Squared)
- Manhattan (L1)
- Dot Product
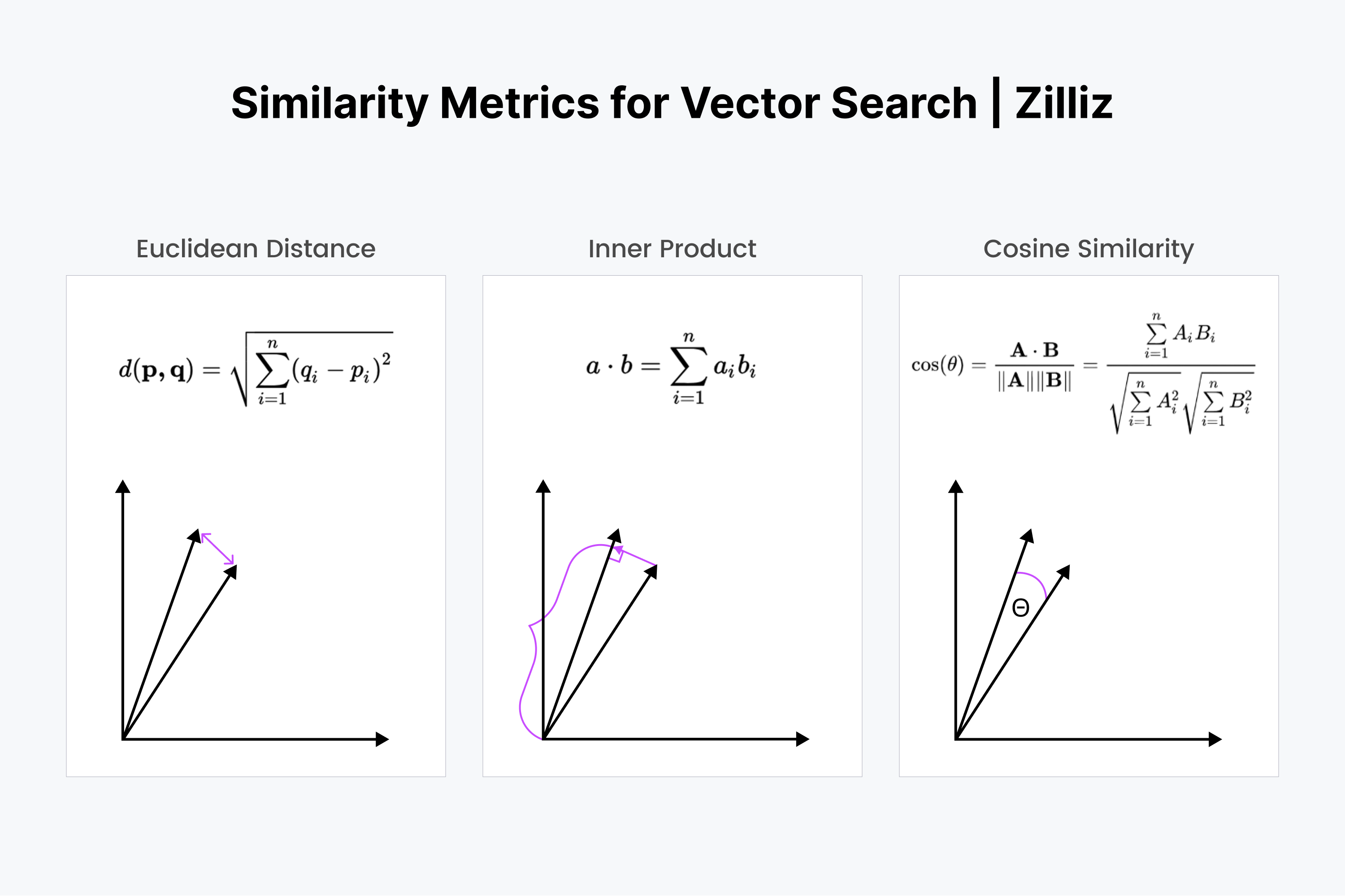Vector similariry figures3
Converting one-hot vector to feature vector
Completing embedding matrix is done by like any other neural network - initializing weights, feed forward and back progagation. Well trained model will output corresponding weight values for each cell in the embedding table.
The number of rows in the table represents the dimension(# of feature) of word embedding vector, for example, 300. Likewise, the number of columns represents the total number of words that are in our represented dictionary, lets say, 10k.
Learning means that each cell is filled with right weight values. Therefore, after the learning process is completed, there will be a corresponding 300 * 10k values in this matrix. Then how can we extract word embedding vector of specific one-hot vector?
The answer is simple dot product(·) of E(embedding table) with O_w(corresponding one-hot vector).
E·O_w = e_w (E: embedding table, O_w: one-hot vector, e_w: word embedding vector)
Note that E is size of 300 * 10k and O_w is size of 10k * 1, resulting e_w which is size of 300 * 1. Note that how 10k dimension vector is shrinked to 300!
Below is an intuitive figure explaining conversion from one-hot vector to word embedding vector:
Conversion from one-hot vector to embedding vectors4
Architecture
Although the basis of word embedding is same, there might be slight differences in details of architecture among word embedding models. In this post we’ll cover word2vec approach, especially CBOW and SkipGram architecture.
CBOW and SkipGrame method diagrams5
CBOW(Continuous Bags of Words)
In CBOW method, neural network is trained such that the model predicts ‘blank’ word in a given context. For example, the model is objected to predict the word that should enter in the blank. → I __ my dog.
SkipGram
In contrast, SkipGram method trains neural network to be trained such that the model predicts ‘context words’ when a word is given. Therefore, the model should produce multiple words as output. For example, when a word ‘dog’ is given, the model should statistically predict the context that goes along with this word.